Tracking a Single Pixel

Nd787 C4 L06 04 Tracking A Single Pixel V1

Math Walkthrough

The diagram below shows a pixel that has moved from (x,y) at time t to (x+u, y+v) at time t+1 .

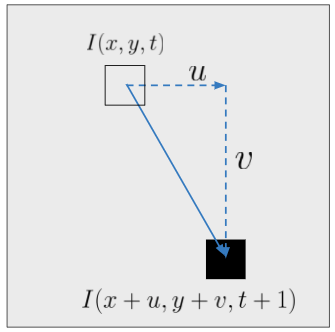
From this picture, it's easy to figure out the velocity vector (u,v) . But when we look at two real images, we'd first need to solve what's called the pixel correspondence problem . That is, we need to know which pixels in image 2 correspond to which pixels in image 1.

To solve this problem we make two assumption.

Assumption 1: the motion is small : this means we can look in the vicinity of where the pixel was to try to determine where it now is .

Assumption 2: the appearance doesn't change from t to t+1 : this assumption is best expressed mathematically.

I(x,y,t) = I(x+u, y+v, t+1)

This relationship is known as the brightness constancy constraint .

If we drop the time index and do a Taylor series expansion of the right hand side of this equation, we find the following:

I(x+u,y+v) \approx I(x, y) + \frac{\partial I}{\partial x} u + \frac{\partial I}{\partial y} v

We can plug this back into the brightness constancy constraint and reorganize some terms to find the following:

\frac{\partial I}{\partial t} + \frac{\partial I}{\partial x} u + \frac{\partial I}{\partial y} v = 0

Or using the notation from the video (which is common in this field):

I_t + I_x u + I_y v = 0

This equation says that any change in the appearance of a pixel over time has to be explained by spatial motion induced by the camera movement.

Note: I(x,y,t) gives the intensity of the pixel at location (x,y) at time t . If this is a gray-scale image, this intensity would be a single number corresponding to the darkness of the pixel. If this were a color image it might be a 3-vector with values giving the amount of red, green, and blue in the image.